Causal Structure Learning
from Event Sequences and Prior Knowledge

Overview

In this competition, the goal is to solve a causal structure learning problem in AIOps (Artificial Intelligence for IT Operations). In telecommunication networks, anomalies are commonly identified through alarms. The network operators might be facing millions of alarms per day due to the large scale and the interrelated structure of the network, as a single fault in the network can trigger a flood of various types of alarms on multiple connected devices. The goal of the operators is to quickly localize the failure point to facilitate a fast repair and recovery. However, to handle all these alarms is exhausting and can quickly overwhelm the operators, and hence it must be done in an intelligent. Recently, there has been increasing interest in tackling the above root cause analysis (RCA) problem from a causal perspective, i.e., learning a causal graph that represents alarm relations and then using decision-making techniques (such as causal effect estimation and counterfactual inference) to efficiently identify the root cause alarm when a fault occurs. A typical RCA solution for the telecommunication network is depicted in Figure 1.

The competition task can be described as follows: Given a series of datasets, for each dataset, participants are supposed to use the historical alarm data, device topology, and prior knowledge (if available) to learn a causal graph for the involved alarm types. Each learned causal graph is represented by a binary adjacency matrix, where the element in the i-th row and j-th column of the matrix equals 1 (0) means the existence (resp. non-existence) of a directed edge from the alarm type i to alarm type j. The ground truth for these causal graphs, i.e. true causal graphs, are labeled manually by experts or, for the synthetic datasets, the pre-set causal assumptions. Please note that all true causal graphs will not be public during the competition. Besides, we recommend competitors design a unified learning solution(algorithm) for handling all datasets. While it’s not mandatory, the generalization of the submitted solution(algorithm) will be an important aspect of evaluating the novelty and will affect the final ranking.

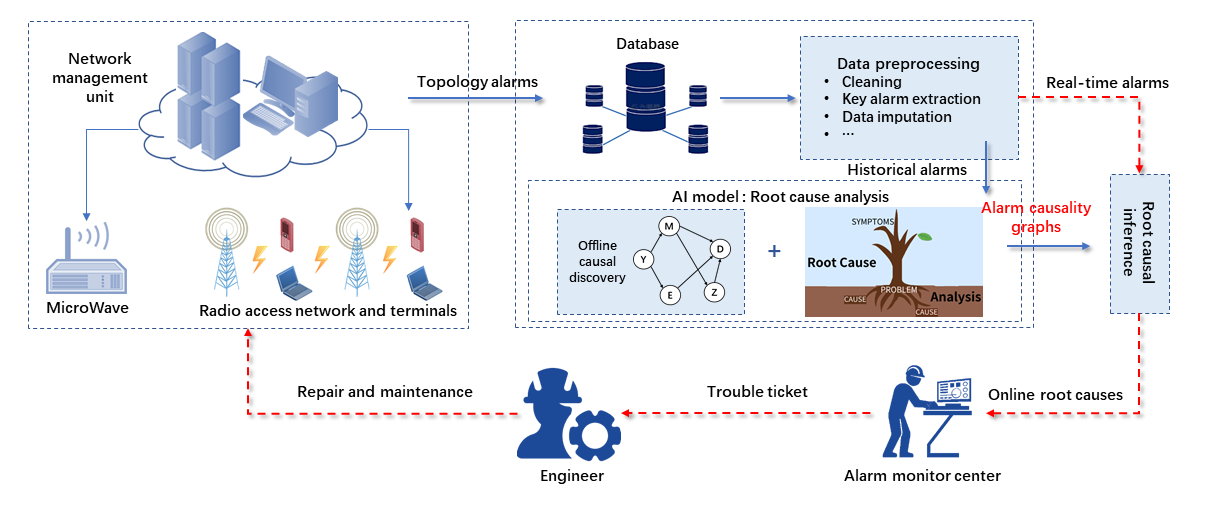
Figure 1: RCA solution in a telecom network

Dataset

This competition includes two types of datasets: artificial datasets and real-world datasets, in which the real-world datasets are collected from a telecommunication network, while the artificial datasets are generated by our internal data simulators which are designed using domain expertise. We plan to divide the competition into two phases and provide a total of six datasets over the entire competition, in which four of the datasets will be released in the first phase and the final two are appended in the second (final) phase. The assignment of the datasets are shown in Table 1

Table 1: Dataset assignment over competition phases.

Phase No.	Dataset
Phase 1	3 simulation datasets + 1 real datasets
Phase 2	1 simulation datasets + 1 real datasets

Dataset information given to the competition participants If you download the datasets from our competition site, you’ll find that K datasets are stored in separated directories named from 1 to K, and each dataset fully or partially includes the following data files:

alarm.csv: Historical alarm data

Format: [alarm_id, device_id, start_timestamp, end_timestamp]
Description: In the alarm data file we provide historic alarm information. Each row denotes an alarm record which contains the alarm ID (i.e., the alarm type), the device where the alarm occurred, the start timestamp, and the end timestamp. For privacy, every alarm id is encoded to an integer number starting from 0 to N-1, where N is the number of the alarm types. Each device ID is likewise encoded to an integer number starting from 0 to M-1, where M is the number of the devices.
Example:
alarm_id device_id start_timestamp end_timestamp
2 28 30684 32416
10 28 30684 30867
13 32 30795 32668
0 35 32215 32867

alarm_id	device_id	start_timestamp	end_timestamp
2	28	30684	32416
10	28	30684	30867
13	32	30795	32668
0	35	32215	32867

topology.npy (Optional): The connections between devices .

Format: an M ×M NumPy array, with M being the number of the devices in the network.
Description: This NumPy file stores the binary symmetric adjacency matrix for the network topology which is an undirected graph. For example, the element which is in the i-th row and j-th column of the matrix equals 1 (0) means the existence (resp. non-existence) of an undirected link between the device i and the device j.
Example : M=4

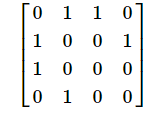
causal_prior.npy (Optional): Prior knowledge indicating definite causal relation information.

Format: An N × N NumPy array, where N is the number of the alarm types.
Description: Similar to the topology, causal_prior.npy stores an adjacency matrix for partially representing the true causal alarm graph. The prior information is labeled manually by experts or, for the synthetic datasets, the pre-set causal assumptions. The element in the i-th row and j-th column of the matrix equals 1 (0/-1), which means the existence (resp. non-existence or Uncertain) of a directed edge from the alarm type i to alarm type j.
Example: N = 3, see Figure 2

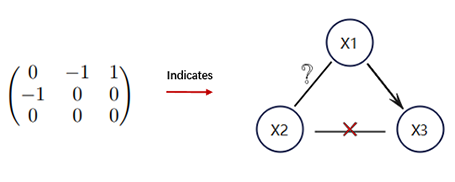
Figure 2: Causal Prior

rca_prior.csv (Optional): Prior knowledge including some simplified fault snapshots and the corresponding RCA results.

Format: [simplified_snapshot, simplified_root_cause]
Description: In the real-world RCA scenario, a fault snapshot contains detailed information on the network state (a series of alarms with occurrence time and occurrence location information) within the period a fault occurs, while simplified fault snapshots extract or compress the corresponding network state to an alarm type list ignoring the occurrence time/location and sequential information, and the corresponding RCA result is as well. Due to considering knowledge reusability, the simplified snapshots along with simplified RCA results (also can be regarded as RCA rules) are a common way to store considerable raw RCA cases in the AIOps field.
Example: see Figure 3

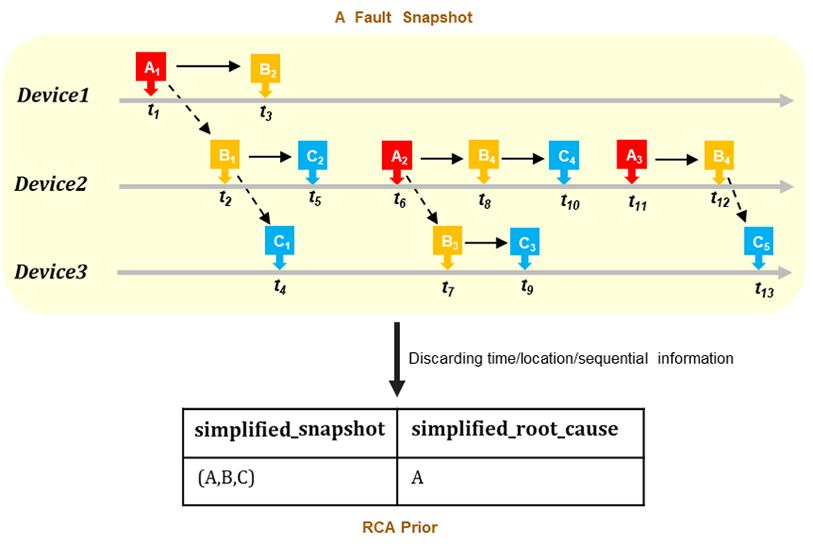
Figure 3: RCA Prior

It’s essential to note that each dataset is causally independent of others, hence it’s not suitable to do any information exchange among these datasets when executing causal discovery tasks.

Evaluation

We evaluate the submitted causal graphs using the metric that we call g-score, which is defined based on real-world requirements and is used internally at Huawei. We want to identify more true causal relations and less false causal relations while being relatively tolerant of being unable to find some of the true causal relations (false negatives). This is a rational setting as the data limit cannot guarantee all causal relations to be founded from data, especially in just partially observed real-world scenarios. The definition of the g-score for an estimated causal graph is as follows:

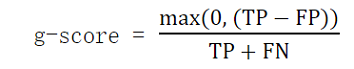
TP (True Positive): A directed edge estimated with correct direction.
FP (False Positive): A directed edge that is in estimated graph but not in the true graph.
FN (False Negative): A directed edge that is not in estimated graph but in the true graph.

Based on the above definition, the corresponding ranking score of a submission will be evaluated as follows:

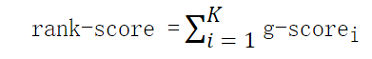
where K is the number of datasets. The maximum rank-score is 1.

Prize

Our competition will provide cash prizes and electrical certificates for winners. The total prize amount (USD) is $10,000.

1st place: $3,000.
2nd and 3rd place: $2,000.
4th, 5th and 6th place: $1000.

Schedule

August 1, 2023: Competition opens.
August 15, 2023 (rescheduled) : The phase 1 starts and submission systems open.
September 30, 2023: Registration and team formation ends.
October 1, 2023: The phase 1 ends and the submission systems close.
October 8, 2023: The phase 2 starts and submission systems open.
October 22, 2023: Competition ends.
October 30, 2023: Winning teams are announced.